Funciones Trigonométricas
La función seno.
La función seno se define a partir del concepto de seno, considerando que el ángulo siempre debe expresarse en radianes. Para representar dicha función, tan sólo deben trasladarse los valores del seno obtenidos a partir de la circunferencia unitaria a la gráfica de la función, tal como puede hacerse en esta aplicación desplazando el punto que representa el valor de x (es decir, el valor del ángulo α) a derecha e izquierda.
* La función coseno.
La función coseno se define a partir del concepto de coseno, considerando que el ángulo siempre debe expresarse en radianes. Para representar dicha función, tan sólo deben trasladarse los valores del coseno obtenidos a partir de la circunferencia unitaria a la gráfica de la función, tal como puede hacerse en esta aplicación desplazando el punto que representa el valor de x (es decir, el valor del ángulo α) a derecha e izquierda.
* La función tangente.
La función tangente se define a partir del concepto de tangente, considerando que el ángulo siempre debe expresarse en radianes. Para poder entender la construcción de su gráfica resulta muy útil, como en el caso del seno y del coseno, ofrecer, en primer lugar, una interpretación gráfica de la tangente.

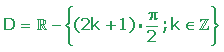
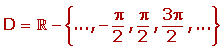







La función seno se define a partir del concepto de seno, considerando que el ángulo siempre debe expresarse en radianes. Para representar dicha función, tan sólo deben trasladarse los valores del seno obtenidos a partir de la circunferencia unitaria a la gráfica de la función, tal como puede hacerse en esta aplicación desplazando el punto que representa el valor de x (es decir, el valor del ángulo α) a derecha e izquierda.
Podemos observar varias características de la función seno:
- Su dominio contiene a todos los reales. En cambio, su imagen es el intervalo [-1,1], ya que el seno de un ángulo siempre se encuentra entre estos valores.
- Esta función se repite exactamente igual cada 2π; es decir, los valores de la función en el intervalo del dominio [0,2π) son suficientes para conocer la función en cualquier punto. Se dice, en este caso, que la función es periódica, deperíodo 2π.
- La función se anula en los valores x iguales a , siendo k un número entero.
- La función alcanza sus extremos máximos, es decir, los valores mayores de la y, cuando el seno del ángulo es 1, es decir, cuando la x es , siendo k un número entero cualquiera. Sus extremos mínimos, es decir, los valores menores de la y (cuando el seno es -1), se encuentran cuando la x es , siendo k cualquier número entero.
* La función coseno.
La función coseno se define a partir del concepto de coseno, considerando que el ángulo siempre debe expresarse en radianes. Para representar dicha función, tan sólo deben trasladarse los valores del coseno obtenidos a partir de la circunferencia unitaria a la gráfica de la función, tal como puede hacerse en esta aplicación desplazando el punto que representa el valor de x (es decir, el valor del ángulo α) a derecha e izquierda.
Podemos observar varias características de la función coseno:
- Su dominio contiene a todos los reales. En cambio, su imagen es el intervalo [-1,1], ya que el coseno de un ángulo siempre se encuentra entre estos valores.
- Esta función se repite exactamente igual cada 2π; es decir, los valores de la función en el intervalo del dominio [0,2π) son suficientes para conocer la función en cualquier punto. Así pues, es periódica, de período 2π.
- La función se anula en , siendo k cualquier número entero.
- La función alcanza sus extremos máximos, es decir, los valores mayores de la y, cuando el coseno del ángulo es 1, es decir, cuando la x es , siendo k un número entero cualquiera. Sus extremos mínimos, es decir, los valores menores de la y (cuando el coseno es -1), se encuentran cuando la x es , siendo k cualquier número entero.
* La función tangente.
La función tangente se define a partir del concepto de tangente, considerando que el ángulo siempre debe expresarse en radianes. Para poder entender la construcción de su gráfica resulta muy útil, como en el caso del seno y del coseno, ofrecer, en primer lugar, una interpretación gráfica de la tangente.
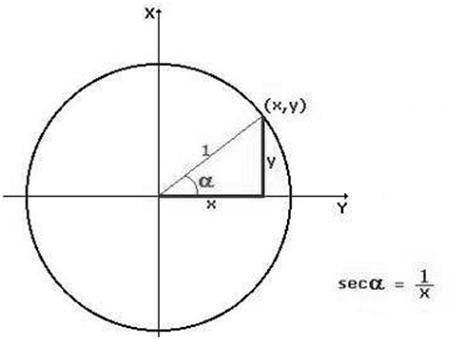
Es evidente que la coordenada y del punto resaltado es la tangente del ángulo, porque su coordenada x es siempre 1, y el cociente de ambas coordenadas ha de ser precisamente la tangente de α:
Para representar dicha función, tan sólo deben trasladarse los valores de la tangente obtenidos a partir de la circunferencia unitaria a la gráfica de la función, tal como puede hacerse en esta aplicación desplazando el punto que representa el valor de x (es decir, el valor del ángulo α) a derecha e izquierda:
Podemos observar varias características de la función tangente:
- Su dominio contiene a todos los reales excepto a aquellos en los que no existe la tangente, que son los ángulos , siendo un número entero. En cambio, cualquier número real pertenece a su imagen.
- Esta función se repite exactamente igual cada π; es decir, los valores de la función en el intervalo del dominio , son suficientes para conocer la función en cualquier punto. Así pues, es periódica, de período π.
- La función se anula en , siendo k un número entero.
- La función no tiene ni máximos ni mínimos porque siempre crece (dentro de su dominio, claro está).
Función Cotangente:
La noción de cotangente alude a la función inversa de la tangentede un arco o de un ángulo. Para comprender qué es la cotangente, por lo tanto, debemos saber qué es la tangente.

En el contexto de la trigonometría (una especialidad de las matemáticas), la tangente de un triángulo rectángulo se obtiene dividiendo el cateto opuesto a un ángulo agudo y el cateto adyacente. Cabe recordar que el lado mayor de estos triángulos se llama hipotenusa, mientras que los otros dos reciben la denominación de catetos.
Retomando la idea de cotangente, ya habíamos mencionado que se trata de la función inversa de la tangente. Por lo tanto, si la tangente es el cociente entre el cateto opuesto y el cateto adyacente, la cotangente equivale al cociente entre el cateto adyacente y el cateto opuesto.
En un triángulo rectángulo cuya hipotenusa mide 20 centímetros, su cateto adyacente mide 15 centímetros y su cateto opuesto mide 12 centímetros, podemos calcular la cotangente de la siguiente forma:
Cotangente = Cateto adyacente / Cateto opuesto
Cotangente = 15 / 12
Cotangente = 1,25
Cotangente = 15 / 12
Cotangente = 1,25
Dado que la cotangente es la función inversa de la tangente, también se la puede obtener dividiendo 1 por la tangente. En nuestro ejemplo anterior, la tangente equivale a 0,8 (el resultado de la división entre el cateto opuesto y el cateto adyacente). Por lo tanto:
Cotangente = 1 / tangente
Cotangente = 1 / 0,8
Cotangente = 1,25
Cotangente = 1 / 0,8
Cotangente = 1,25
Así como la cotangente es la función inversa de la tangente, la cosecante es la inversa del seno y la secante, la inversa del coseno.
Función Secante:
Está representada como y=sec(x), y es también la inversa del coseno:
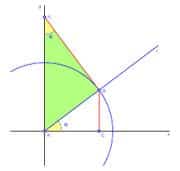
En un triángulo rectángulo, es la longitud de la hipotenusa dividida para la longitud del lado adyacente.

Observemos ahora la función secante y su definición como función circular:
para lo cual recurrimos al siguiente gráfico.

La “secante circular del ángulo a”, o, simplemente, “secante de a”
La función no tiene ceros ya que para que de existir tendría que poder anularse el numerador de la fracción 1/cos x y eso no ocurre nunca porque es una constante:
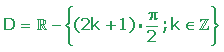
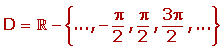
Por último me gustaría mostraros la representación gráfica:

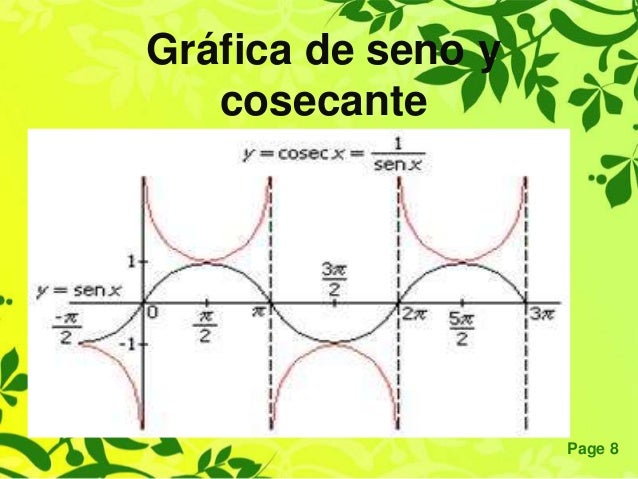
Función Cosecante:
La cosecante es la razón trigonométrica inversa del seno. Es el inverso multiplicativo del seno, es decir csc α · sen α=1.
La cosecante del ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto opuesto (a).
Su abreviatura es csc o cosec.
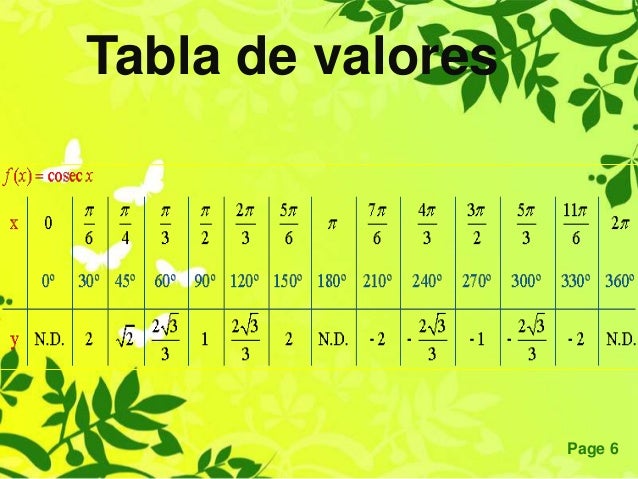
Cosecante de ángulos característicos
La cosecante de los ángulos más característicos es:
Características de la cosecante
- Dominio de la función:
- Recorrido de la función:
- Derivada de la función:
- Integral de la función:
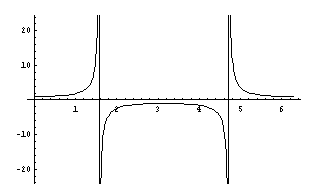
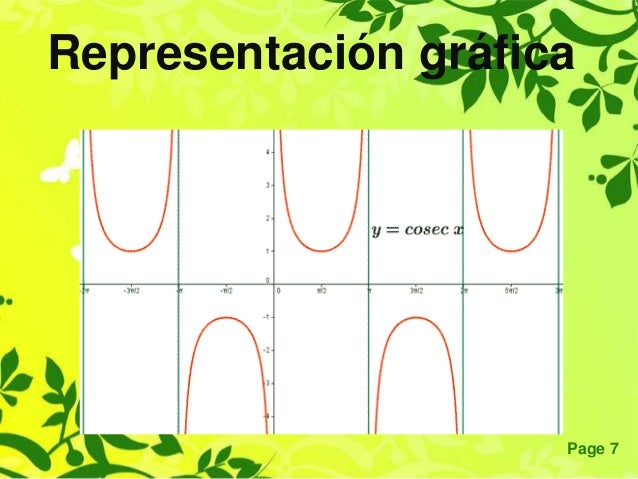
Representación gráfica de la función cosecante
La función es periódica de período 360º (2π radianes), por lo que esta sección de la gráfica se repetirá en los diferentes períodos.
Representación geométrica
Relaciones con las restantes razones trigonométricas
- Relación con el seno:
- Relación con el coseno:
- Relación con la tangente:
- Relación con la secante:
- Relación con la cotangente:




Comentarios
Publicar un comentario