Funciones Algebráicas

Función Constante:

La función constante es del tipo:

y = n

El criterio viene dado por un número real.

La pendiente es 0.

La gráfica es una recta horizontal paralela a al eje de abscisas.

Función lineal:

Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.

La función lineal se define por la ecuación f(x) = mx + b ó y = mx + b llamada ecuación canónica, en donde m es la pendiente de la recta y b es el intercepto con el eje Y.

Por ejemplo, son funciones lineales f(x) = 3x + 2 g(x) = - x + 7 h(x) = 4 (en esta m = 0 por lo que 0x no se pone en la ecuación).

Esta es la gráfica de la función lineal y = 3x + 2

Vemos que m = 3 y b = 2 (de la forma y = mx + b)

Función Cuadratica:

Una función cuadrática es un polinomio de grado 2, es decir, el exponente más alto en la variable es 2. Los siguientes son ejemplos de funciones cuadráticas:

La función cuadrática más básica y simple tiene la ecuación 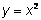. Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática:

x	y = x2
-3	9
-2	4
-1	1
0	0
1	1
2	4
3	9

Los valores de y no cambian por una cantidad constante. Grafiquemos algunos puntos para ver cómo se vería la función:

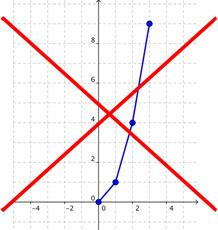
Después de graficar algunos puntos, podría ser tentador conectar los puntos con segmentos de línea, que son rectos. Pero esto estaría mal, y produciría un patrón que no representa la función.

Borremos esas líneas rectas y grafiquemos el resto de los puntos:

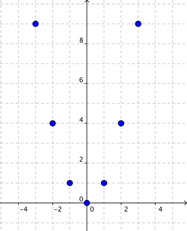
Ahora dibujamos una curva suave conectando los puntos.

 La función cúbica se define como el polinomio de tercer grado; el cual se expresa de la forma: f(x) = ax3 + bx2 + cx + d con a ≠ 0, a, b, c y d Œ IR

Función Cúbica:

Un ejemplo de función cúbica es: y = f(x) = x3, es la llamada: parábola cúbica. 

Propiedades

• El dominio de la función es la recta real es decir (-α : α)
• El recorrido de la función es decir la imagen es la recta real.
• La función es simétrica respecto del origen, ya que f(-x)=-f(x).
• La función es continua en todo su dominio.
• La función es siempre creciente.
• La función no tiene asintotas.
• La función tiene un punto de corte con el eje Y.
• La función puede tener hasta un máximo de 3 puntos de intersección con el eje X.

Ejemplos

Grafique y analice las propiedades de la siguientes funciones

a) f(x) = 2x3 + 3x2 - 12x

Propiedades

• Dominio: El conjunto de los Reales
• Imagen: El conjunto de los Reales
• Ceros de la función:

Se iguala la función a cero

2x3 + 3x2 - 12x = 0 x( 2x2 + 3x - 12) = 0 Extrayendo factor común x = 0 ( 2x2 + 3x + 12)= 0 Igualando a cero ambos factores y realizar la descomposición.

• Simetría: Demostrar que cumple f(-x)=-f(x).

Para demostrar la simetría analíticamente de selecciona un número cualesquiera y su opuesto ejemplo 1 y -1 Demostrar que f(-1) = - f(1)

f(-1) = 2(-1)3 + 12 . (-1)2 + 2. (-1 )

      =  2.(-1)  + 12 . 1  - 2   
      =  -2  + 12  -  2  
      =  10 - 2 
      =  8 

f(1) = 2(1)3 + 12 . (1)2 + 2. (1 )

      =    2.(1)  -  12 . 1  +  2 
      =    2  - 12 + 2 
      =   -10 + 2  
      =  -8 

Como f(-1) = - f(1) por tanto la función es simétrica.

• Continuidad: La función es continua en todo su dominio pues gráficamente se puede observar que no tiene ningún punto de discontinuidad.
• La función no tiene asintotas.

• Para determinar los puntos donde la función corta el eje de la y

Se determina el valor de la función para x=0 f(0) = 2. 03 + 3. 02 - 12. .0 Obteniendo y= 0 y la función corta el eje de la y en el punto (0:0)

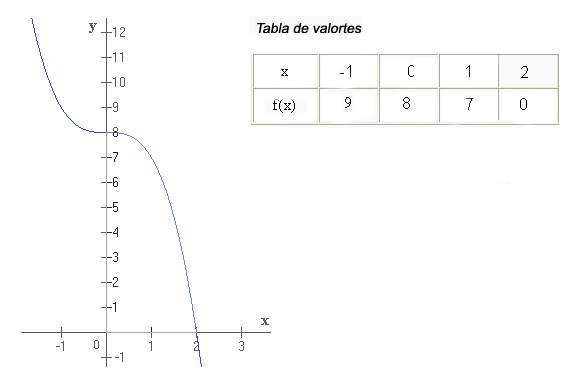
b) F(x) = -x3 +8

Función Radical:

Las funciones radicales son aquellas en las que la variable se encuentra bajo el signo radical. En esta práctica estudiaremos las funciones del tipoy también las que tienen como expresión general .

La gráfica de estas funciones es muy diferente a las de las anteriormente estudiadas.

 

En primer lugar, son funciones positivas, pues en la definición de la función se considera únicamente la raíz positiva del radicando.

(Si la expresión algebraica de la función fuera entonces serían funciones que sólo tomarían valores negativos)

En segundo lugar, si observas las gráficas representadas podrás ver que, en muchas ocasiones, sólo están definidas en un tramo de la recta real; en estos casos su dominio de definición no son todos los números reales ya que la raíz cuadrada sólo está definida para valores positivos del radicando.

Por último, su comportamiento respecto a la monotonía (crecimiento y decrecimiento) es bastante sencillo.

En esta práctica vamos a estudiar las propiedades fundamentales de los dos tipos de funciones radicales:  y  .

QUÉ HACER

En la primera escena puedes ver la gráfica de la función  para los valores en los que estén situados los deslizadores.

En primer lugar analizarás las propiedades de las funciones del tipo , para lo que situarás el deslizador a en el valor 0. Moviendo los otros deslizadores estudiarás:

–         El dominio de definición de la función.

–         El crecimiento o decrecimiento de la misma.

–         La existencia de extremos relativos (máximos y mínimos).

Después estudiarás estas propiedades para las funciones del tipo  situando el deslizador a en valores no nulos. 

Función Proporcional:

Cuando las variables independiente y dependiente son proporcionales, es decir cuando aumenta la variable independiente la variable dependiente lo hace en la misma proporción, y cuando disminuye la variable independiente la variable dependiente lo hace también en la misma proporción, entonces la función que las relaciona se dice que es de proporcionalidad directa.

Ejemplo: supongamos la función y = 2x

Este tipo de funciones en los que la variable dependiente es igual a la variable independiente multiplicada por un coeficiente, su representación gráfica es una recta.

Función Racional:

Una función racional es una función que puede escribirse como cociente de dos polinomios.

Si el denominador es un número (un polinomio de grado 0), entonces la función es un polinomio. Por lo tanto, las funciones polinómicas son funciones racionales. En estas páginas sobre funciones racionales vamos a considerar solamente funciones racionales cuyo denominador es un polinomio de grado mayor que 0.

Las funciones racionales pueden tener características que las diferencian de las funciones polinómicas y que vamos a revisar en estas páginas:

- Singularidades: En algunos casos, algunos valores de x son problemáticos. Esto es debido a que las funciones racionales hay un denominador que puede ser 0 y no podemos dividir entre 0. Esos valores de x que hacen 0 el denominador juegan un papel especial. Como no podemos calcular el valor de la función en esos valores decimos que la función no está definida para esos valores de x.

También decimos que esos puntos no pertenecen al dominio de la función. El dominiio de una función racional está determinado por las restricciones impuestas por el denominador: dividir entre 0 es imposible.

El dominio es el conjunto de los números reales para los que la función está definida. En el caso de las funciones racionales es el conjunto de todos los números reales que no son ceros del denominador. Por lo tanto, para determinar el dominio de una función racional tenemos que encontrar los ceros reales del denominador.

A estos puntos se les llama singularidades y es interesante ver cómo se comporta la función cerca de esos puntos.

- Puntos de corte con el eje de abcisas: Se trata de encontrar los valores de x que hacen que el gráfico de la función cruce el eje de abcisas. Son los valores de x para los que f(x)=0.

- Continuidad: Las funciones racionales son continuas en su dominio (pero su dominio puede no ser todos los números reales).

- Comportamiento "en el infinito": Es interesante el estudio del comportamiento de la función cuando x se hace más y más grande en valor absoluto (siendo x positivo o negativo). Veremos que en algunos casos la función se aproxima a una recta (horizontal u oblicua). En estos casos diremos que la función tiene una asíntota horizontal u oblicua (según los casos). En todos los casos el comportamiento de una función racional "en el infinito" está determinado por una función polinómica.

Función De Orden Superior: